第一列
To build a universal quantum computer, one may implement a set of universal gates to approximate any quantum algorithm in the circuit model. However, current physical experiments have only quantum gates with insufficient fidelity and short qubit lifetime. Techniques from quantum error correction (QEC) and fault-tolerant quantum computation (FTQC) are necessary in physical implementations for realizing meaningful quantum computation. In this project, we will study the following aspects of quantum information processing: The primary goal of this project is to construct a practical blueprint of FTQC scheme for near-term quantum devices based on the concatenation of surface and GKP states. FTQC operations will be designed and optimized. Soft-decision decoding of this concatenated schemed using belief propagation will be developed.
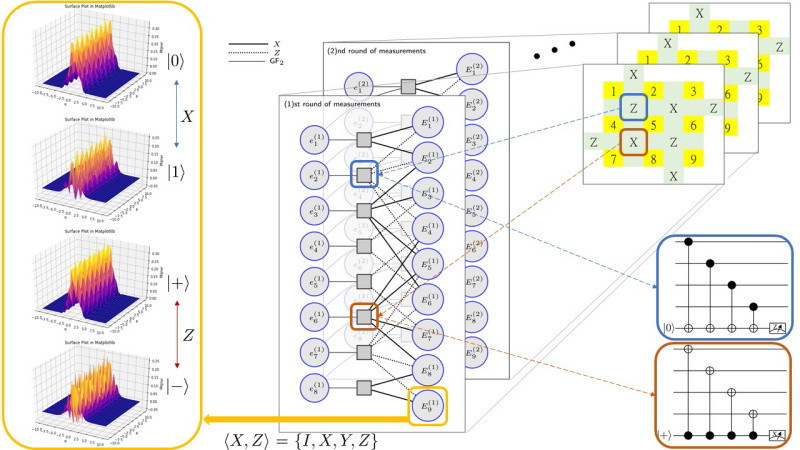
The concatenation of surface-GKP codes. A surface code (right-upper) is composed of physical qubits on a 2D layout, where each physical qubit is a harmonic oscillator, encoded in the GKP code (left). Decoding is done by massage passing on the sequential factor graphs (middle) for decoding with stabilizer syndrome measurements (right-lower).
Belief propagation decoder with a memory effect
Traditional belief propagation (BP) decoders are highly effective in modern communication systems, but they cannot efficiently handle the aforementioned quantum codes with geometric properties. To address the issue of BP algorithms being ineffective for quantum codes, we introduced memory effects from mathematical theory. This allows the BP algorithm to resist the propagation of erroneous information while enhancing the algorithm's convergence to find equivalent solutions.
We modified a crucial step of the original BP algorithm, incorporating mathematical memory effects. This significantly improves the decoding performance of BP for quantum codes, representing a major breakthrough in a problem that has been challenging for over a decade. More importantly, this decoder can be applied to general quantum codes.
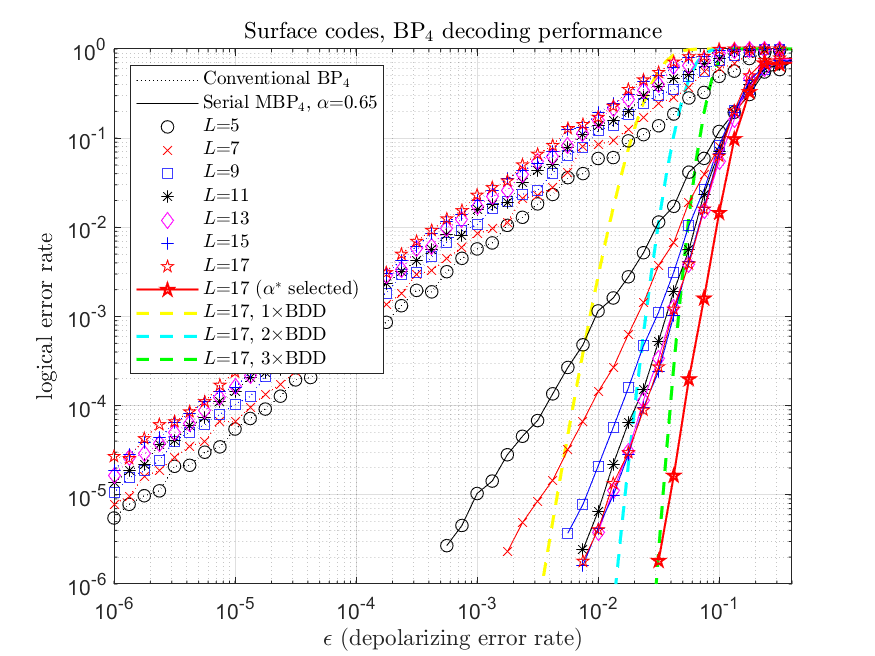
The decoding performance of quantum surface codes using traditional BP and our improved MBP. It is evident that MBP significantly improves upon the traditional BP, which struggles with decoding quantum surface codes.
Reference: npj Quantum Information, 8, Article number: 111, 2
